
Chapter 3 and Chapter 5 study note of Ray Tracing: the Next Week. (Chapter 4 covered in previous post about Perlin Noise.) Implemented functionalities for generic solid texture and image texture mapping.
Texture
A texture in graphics is basically a function that makes the colors on a surface procedural. This procedure can be:
- synthesis code
- image lookup
- or even a video lookup in realtime graphics
Texture Base Class and Constant Color Texture Subclass
From now we start to consider geometry’s color property as being assigned a texture with solid color - a constant color texture.
First of all we make an Abstract Base Class texture. It has only one Pure Virtual Function that return the texture color value, which will be implemented in all subclasses.
C++ Note: Here
value()is a const, pure virtual, member function. Putting const after a member function indicates that the code inside it will not modify the containing object (except in the case of mutable members). More deeply, the purpose of that const is to modify the type of the implicit THIS pointer.
#ifndef TEXTURE_H
#define TEXTURE_H
// a big refactoring of colors
class texture {
public:
virtual vec3 value(float u, float v, const vec3& p) const = 0;
};
#endif //TEXTURE_H
Then we derive the constant color texture class from this base. It contains color property as class member variable and the value() function is simply implemented to return the color value.
#ifndef CONSTANT_TEXTURE_H
#define CONSTANT_TEXTURE_H
#include "texture.h"
class constant_texture : public texture {
public:
constant_texture() {}
constant_texture(vec3 c) : color(c) {}
virtual vec3 value(float u, float v, const vec3& p) const {
return color;
}
vec3 color;
};
#endif // CONSTANT_TEXTURE_H
Now we can change all albedo from vec3 color to texture pointer texture *albedo.
#ifndef LAMBERTIAN_H
#define LAMBERTIAN_H
#include "material.h"
class lambertian : public material {
public:
lambertian(texture *a) :albedo(a) {} // change from lambertian(const vec3& a) to this
bool scatter(const ray& r_in, const hit_record& rec, vec3& attenuation, ray& scattered) const{
vec3 target = rec.p + rec.normal + random_in_unit_sphere();
scattered = ray(rec.p, target - rec.p, r_in.time());
attenuation = albedo->value(rec.u, rec.v, rec.p); // change from attenuation = albedo to this
return true;
}
texture *albedo; // change from vec3 albedo to this
};
Generated Checker Texture
We make it as another subclass that derived from texture base class. We are also making the dark and light parts of the checker pattern as different solid color textures texture *odd and texture *even.
#ifndef CHECKER_TEXTURE_H
#define CHECKER_TEXTURE_H
#include "texture.h"
class checker_texture : public texture {
public:
checker_texture() {}
checker_texture(texture *t0, texture *t1) : even(t0), odd(t1) {}
virtual vec3 value(float u, float v, const vec3& p) const {
float sines = sin(10 * p.x()) * sin(10 * p.y()) * sin(10 * p.z());
if (sines < 0)
return odd->value(u, v, p);
else
return even->value(u, v, p);
}
texture *odd;
texture *even;
};
#endif //CHECKER_TEXTURE_H
And to apply it to the floor sphere:
texture *checker = new checker_texture(
new constant_texture(vec3(.1, .1, .1)),
new constant_texture(vec3(.5, .5, .5)));
// floor sphere
list[0] = new sphere(vec3(0, -(big_r + 0.5), z), big_r, new lambertian(checker));

At this moment the book mentions
Those checker odd/even pointers can be to some other procedural texture. This is in the spirit of shader networks introduced by Pat Hanrahan back in the 1980s.
which is a great low-level example of my daily work in Unreal material editor:
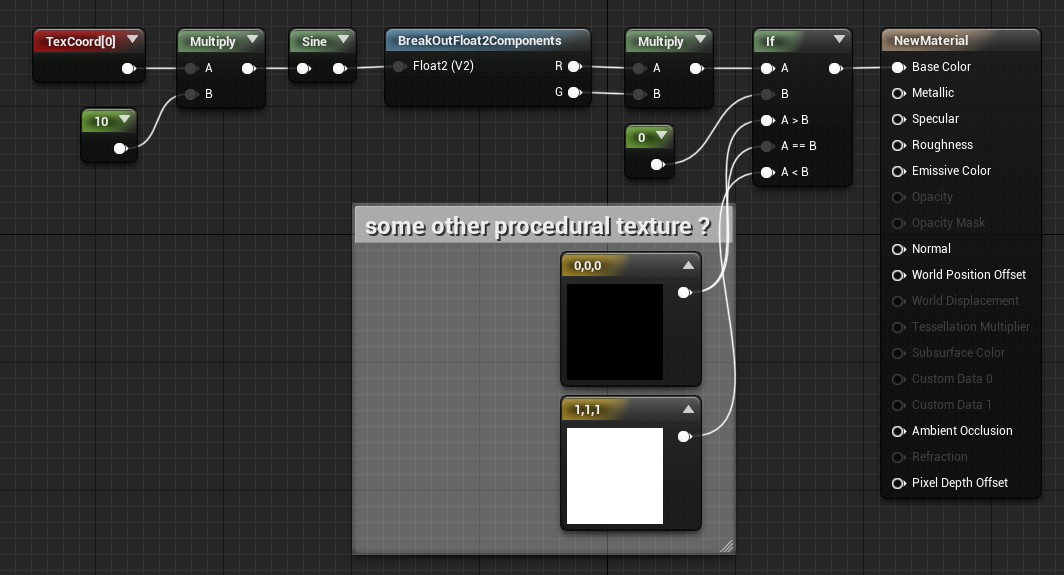
Note that what the code implemented is a 3D checker texture which does not have a proper UV mapping like this Unreal material example. The difference is like this:

Image Texture Mapping
UV Texture Coordinates
In previous section the function virtual vec3 value(float u, float v, const vec3& p) const simply return the color value and the arguments it takes are not used yet. (Actually vec3& p was used to index the generated perlin noise texture in previous post.) Here u, v are needed as texture coordinates to index the image pixel of the texture (or texel).

UV coordinates are easier to use that raw pixel coordinates, as they normalized the coordinates to $[0, 1]$ to avoid dealing with various texture size. The relation is: for pixel $(i, j)$ in an $nx * ny$ image, its UV coordinates are,
\[u = i / (nx - 1)\] \[v = j / (ny - 1)\]But how UV coordinates relate to the hit point $(x, y, z)$ on the sphere? Here we use spherical coordinates $(\theta, \phi)$, where $\theta$ is the angle down from the pole, and $\phi$ is the angle around the axis through the pole. Now the hit point coordinates can be represented as
\[x = cos(\phi)cos(\theta)\] \[y = sin(\phi)cos(\theta)\] \[z = sin(\theta)\]to get the $(\theta, \phi)$ coordinates, we need to invert these: (functions are from math.h, the angles returned are in the range $[-\pi/2, \pi/2]$)
After normalization to $[0, 1]$:
\[u = \phi / 2\pi\] \[v = \theta / \pi\]the image pixel coordinates $(i, j)$ are mapped to hit point coordinates $(x, y, z)$. UV coordinates $(u, v)$ is the bridge.
All these computation for UV coordinates can be packed into an utility function get_sphere_uv()
#ifndef M_PI
#define M_PI 3.14159265358979323846
#endif
static void get_sphere_uv(const vec3& p, float& u, float& v){
float phi = atan2(p.z(), p.x());
float theta = asin(p.y());
u = 1 - (phi + M_PI) / (2 * M_PI);
v = (theta + M_PI / 2) / M_PI;
}
This function is located at hitable.h, where we add uv coordinates into hit_record struct:
struct hit_record{
float t; // hit point distance parameter for ray
vec3 p; // hit point position info, calculated with rec.p = r.point_at_parameter(rec.t);
vec3 normal; // hit point normal info for shading
float u, v; // uv info for image texturing
material *mat_ptr;
};
Read image
The book is using an open source image utility library stb_image.h (link) to read the image. It reads it into a big array of unsigned char. These re packed RGB values each has the range [0, 255].
Now first we are making a new texture subclass for image texture, which has the member variables take the image data array and image dimentions.
Here in the implementation of value() function, we unpack the image data array 3 by 3 with pixel coordinates. The pixel coordinates are derived from the uv coordinates that provided by hitable struct. Then the [0,255] RGB values are normalized to [0,1] and returned as vec3 color value.
#ifndef IMAGE_TEXTURE_H
#define IMAGE_TEXTURE_H
#include "texture.h"
class image_texture : public texture {
public:
image_texture() {}
image_texture(unsigned char *pixels, int A, int B) : data(pixels), nx(A), ny(B) {}
virtual vec3 value(float u, float v, const vec3& p) const;
unsigned char *data;
int nx, ny;
};
vec3 image_texture::value(float u, float v, const vec3& p) const {
int i = ( u)*nx;
int j = (1 - v)*ny - 0.001;
if (i < 0) i = 0;
if (j < 0) j = 0;
if (i > nx - 1) i = nx - 1;
if (j > ny - 1) j = ny - 1;
float r = int(data[3 * i + 3 * nx*j] ) / 255.0;
float g = int(data[3 * i + 3 * nx*j+1]) / 255.0;
float b = int(data[3 * i + 3 * nx*j+2]) / 255.0;
return vec3(r, g, b);
}
#endif
Final Rendering
The final planet scene setup. Note that the specific function used to read the image is stbi_load() from stb_image.h.
texture *checker = new checker_texture(
new constant_texture(vec3(.1, .1, .1)),
new constant_texture(vec3(.5, .5, .5)));
// floor sphere
list[0] = new sphere(vec3(0, -(big_r + 0.5), z), big_r, new lambertian(checker));
int nx1 = 1000, ny1 = 500;
int nx2 = 1024, ny2 = 512;
int nx3 = 960, ny3 = 480;
int nx4 = 2048, ny4 = 1024;
int nn = 3;
// unsigned char *data = stbi_load(filename, &x, &y, &n, 0);
// ... process data if not NULL ...
// ... x = width, y = height, n = # 8-bit components per pixel ...
// ... replace '0' with '1'..'4' to force that many components per pixel
// ... but 'n' will always be the number that it would have been if you said 0
unsigned char *tex_data1 = stbi_load("earth.jpg", &nx1, &ny1, &nn, 0); // pass by reference
unsigned char *tex_data2 = stbi_load("moon.jpg", &nx2, &ny2, &nn, 0);
unsigned char *tex_data3 = stbi_load("mars.jpg", &nx3, &ny3, &nn, 0);
unsigned char *tex_data4 = stbi_load("jupiter.jpg", &nx4, &ny4, &nn, 0);
// image_texture(unsigned char *pixels, int A, int B) : data(pixels), nx(A), ny(B) {}
material *earth_mat = new lambertian(new image_texture(tex_data1, nx1, ny1)); // pass by copy
material *moon_mat = new lambertian(new image_texture(tex_data2, nx2, ny2));
material *mars_mat = new lambertian(new image_texture(tex_data3, nx3, ny3));
material *jupiter_mat = new lambertian(new image_texture(tex_data4, nx4, ny4));
list[1] = new sphere(vec3(-.8, 0, z), 0.5, earth_mat);
list[2] = new sphere(vec3(-.1, -0.3, z), 0.2, moon_mat);
list[3] = new sphere(vec3(.8, -0.2, z), 0.3, mars_mat); //list[3] = new sphere(vec3(1, 0, z), 0.5, new metal(vec3(0.8, 0.8, 0.8), 0.3)); //0.5
list[4] = new sphere(vec3(.3, .5, z-1), 1, jupiter_mat);